The Equations
RN,
the net radiation at the surface equals half of the effective emission
at the TOA, under clear-sky conditions, representing a discontinuity at
the surface in radiative equilibrium and the convective fluxes (sum of
latent heat and sensible heat) in radiative-convective equilibrium:
This equality is referred to explicitly or implicitly in every standard university textbooks on atmospheric physics and radiation as a consequence of Schwarzschild's (1914) radiative eequilibrium model, especially of his original (1906) two-stream equation (11), but it is missing from all the climate papers is journal articles. We will try to find out why.
Manabe-Möller (1961, Monthly Weather Review, MWR) refer to Gold (1909, Proceedings, PRSA) and Emden (1913, Sitzungsberichte). Manabe-Strickler (1964) only to Emden (1913); but none of them to Schwarzschild.
Emden (1913) refers to Schwarzschild (1906, Nachrichten) and Gold (1909). Gold does not refer to Schwarzschild. Schwarzschild (1906) gives the two-stream radiative transfer equations for radiative equilibrium conditions in the Sun's atmosphere; Gold deals exclusively with Earth's atmosphere and the thermal and radiative conditions of convective equilibrium.
As a matter of fact, convective equilibrium was mentioned earlier by Sampson (1894, Proc Royal Astron Soc), and the two-stream radiation transfer equations were given by Schuster (1905, Astrophys. J).
Emden (1913) became available in English in 1916 (MWR). The Translator of the paper emphasizes the relation of Emden's work to Gold's, for several reasons. In the table of content (Inhaltsübersicht) of Emden's paper, Schwarzshild's name does not occur, only Humphrey and Gold; he refers to Schwarzschild as the first who brought the state of equilibrium to attention and to Gold as who started from similar points of view; repeats Schwarzschild's equations, then analyzes the works of Humphrey and Gold on the temperature of the stratosphere.
Worth to note that Schwarzschild's equation (1906, eq. 11) is reproduced in slighly different structure by Emden than the original.
Schwarzschild's equation (1906, eq. 11) is this (E is the blackbody emission of a layer, A is the upward beam, B is the downward beam, A0 is the emerging flux at the top of the atmosphere, and m is the 'Optische masse', optical depth):
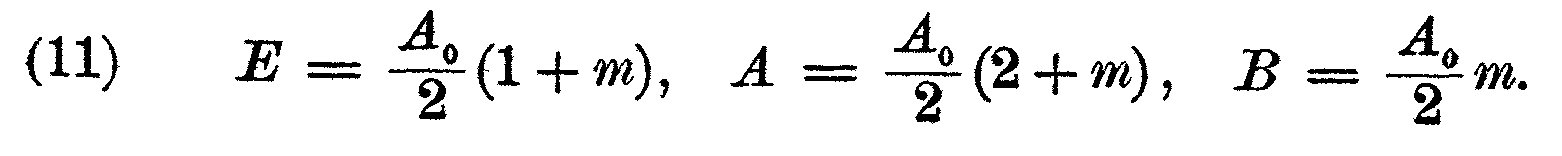In Emden's paper, it is given in this form:
RN
(clear-sky) = Surface (SW + LW) net = LH + SH = Outgoing LW/2 .
This equality is referred to explicitly or implicitly in every standard university textbooks on atmospheric physics and radiation as a consequence of Schwarzschild's (1914) radiative eequilibrium model, especially of his original (1906) two-stream equation (11), but it is missing from all the climate papers is journal articles. We will try to find out why.
Manabe-Möller (1961, Monthly Weather Review, MWR) refer to Gold (1909, Proceedings, PRSA) and Emden (1913, Sitzungsberichte). Manabe-Strickler (1964) only to Emden (1913); but none of them to Schwarzschild.
Emden (1913) refers to Schwarzschild (1906, Nachrichten) and Gold (1909). Gold does not refer to Schwarzschild. Schwarzschild (1906) gives the two-stream radiative transfer equations for radiative equilibrium conditions in the Sun's atmosphere; Gold deals exclusively with Earth's atmosphere and the thermal and radiative conditions of convective equilibrium.
As a matter of fact, convective equilibrium was mentioned earlier by Sampson (1894, Proc Royal Astron Soc), and the two-stream radiation transfer equations were given by Schuster (1905, Astrophys. J).
Emden (1913) became available in English in 1916 (MWR). The Translator of the paper emphasizes the relation of Emden's work to Gold's, for several reasons. In the table of content (Inhaltsübersicht) of Emden's paper, Schwarzshild's name does not occur, only Humphrey and Gold; he refers to Schwarzschild as the first who brought the state of equilibrium to attention and to Gold as who started from similar points of view; repeats Schwarzschild's equations, then analyzes the works of Humphrey and Gold on the temperature of the stratosphere.
Worth to note that Schwarzschild's equation (1906, eq. 11) is reproduced in slighly different structure by Emden than the original.
Schwarzschild's equation (1906, eq. 11) is this (E is the blackbody emission of a layer, A is the upward beam, B is the downward beam, A0 is the emerging flux at the top of the atmosphere, and m is the 'Optische masse', optical depth):
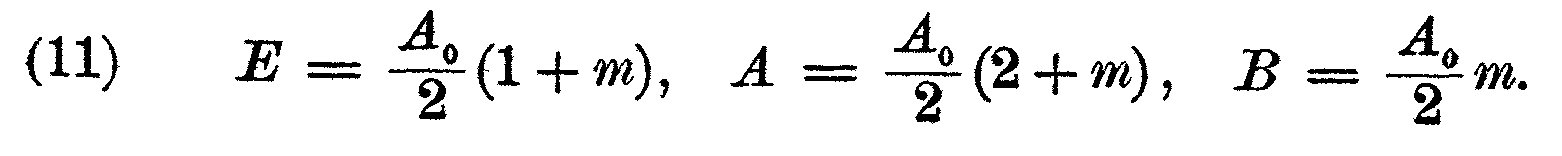
The English translation
repeats the differential equations, and the solution is given in the
specified form for Gold's problem.
While in Schwarzschild's original terms it is evident from one sight that the difference of A and E, the net radiation at the lower boundary, is unequivocally equal to A0/2, independently of the optical depth, it is less straightforward in Emden's formulation of the solution, and even less obvious in the English translation.
Therefore, from the viewpoint of Manabe-Moller and Manabe-Strickler, the emphasis in this research was not on Schwarzschild's equations, but on Emden's solution. But with this shift of focus, the right-hand side of the equation, its constrained character, and the prescribed magnitude, finally disappeared.
The books an atmospheric physics and radiation brought back Schwarzshild's equations into the attention, but the climate papers went on computing temperature changes by the greenhouse gases and simulated Earth's climate through computer models, where the changes in convection were functions of the surface temperature, but not restricted by radiative transfer constraints. Manabe (971), Manabe and Wetherald (1967, 1975, 1980) are talking about climate sensitivity without mentioning the existence of the constrained character of surface net radiation.
Their followers, Ramanathan and Coakley (1978), Ramanathan et al. (1979), and The Charney Report (1979) do not refer to Schwarzshild's constraint, although at that time it was already there in Goody (1964, Mentzel (1967), Houghton (1977), Chamberlain (1978), and so on.
And finally, it it missing from all the IPCC Reports (1990-2021).
In 1991, Dr. Graeme Stephens had a huge opportunity to re-introduce Schwarzschild to the climate community. When the GEWEX project was initiated, he wrote four papers in the Earth's radiation budget and its relation to atmospheric hydrology (JGR), and in the first paper he took the equations from Mihalas (1978) and from Goody and Yung (1989), in this form:
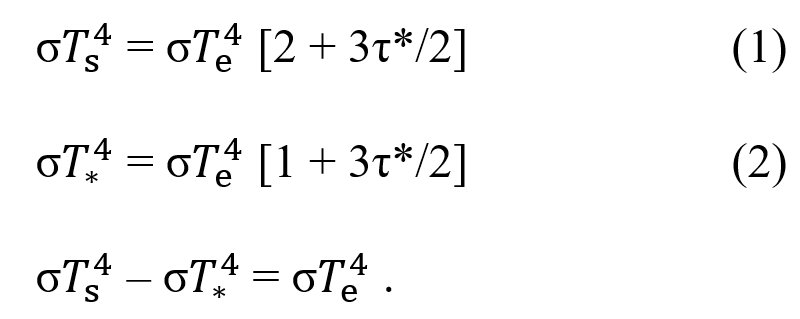The
first equation is the upward beam (the second term) in Schwarzshild
(1906, eq. 11), and the second equation is the emission at the surface
(the first term); therefore their difference must give the net
radiation at the surface (the third, unnumbered equation). But because
of a technical misuse, a division by two was lost on the right-hand
side, therefore the third (unnumbered) equation incorrectly connects
net radiation at the surface to the effective emission, thus their data
evidently didn't fit, so this approach proved unuseful.
The fourth paper of the series (1994) gives the equations correctly:
Here the first equation is still the middle-term is Schwarzschild (1906, eq.11), but the second equation is not the first term (the emission of the layer), but the third term (the downward emission). So here the net radiation can be calculated correctly is F∞/2, but it is not expressed explicitly. This problem could have been avoided if he took the equations directly from Schwarzschild.
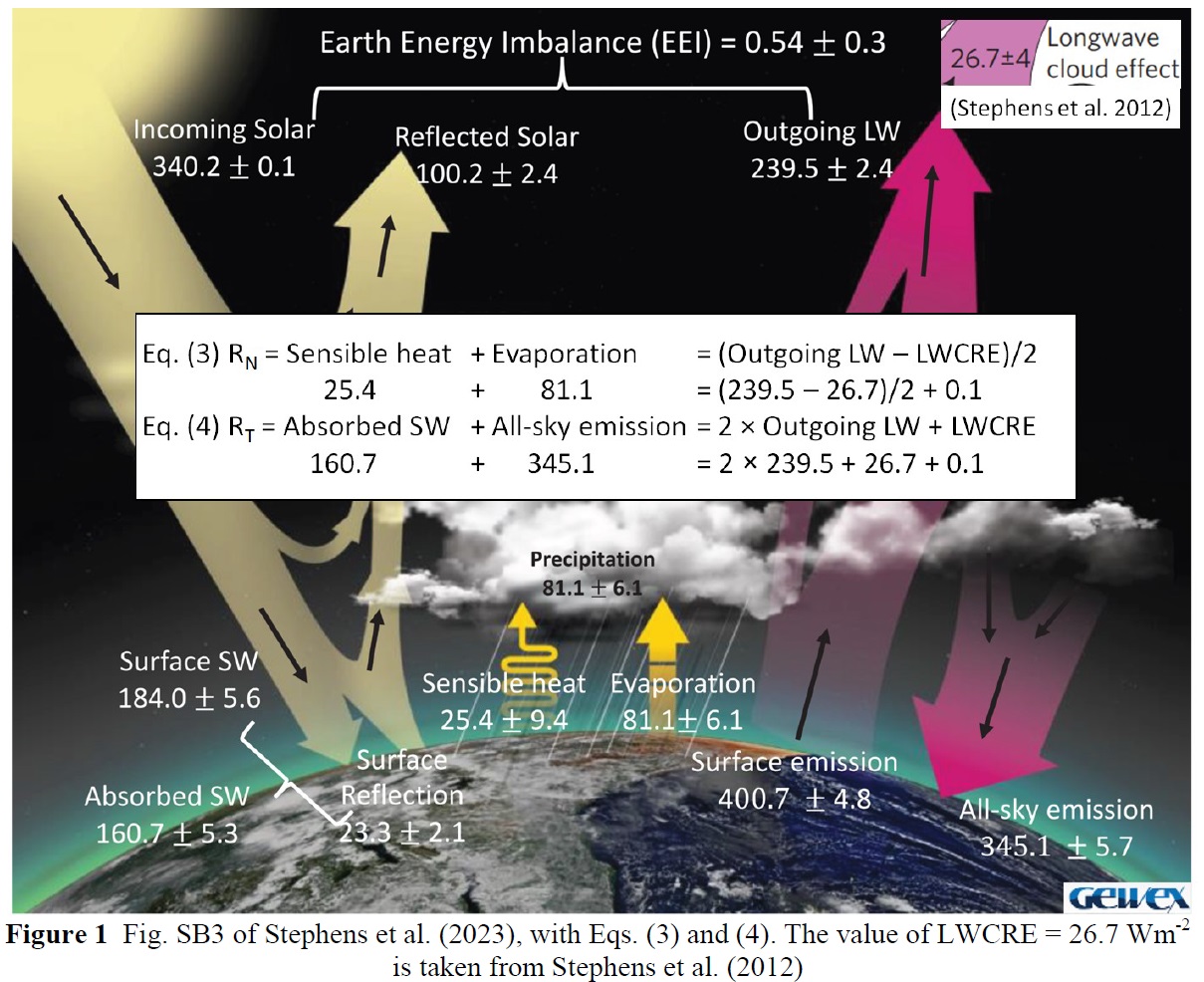
But finally, the all-sky version of this equation, together with its total-energy counterpart, is verified with a difference of 0.1 Wm-2 in the most recent, and most comprehensive study on 30 years of GEWEX, by Stephens and Coauthors (2023, BAMS).
While in Schwarzschild's original terms it is evident from one sight that the difference of A and E, the net radiation at the lower boundary, is unequivocally equal to A0/2, independently of the optical depth, it is less straightforward in Emden's formulation of the solution, and even less obvious in the English translation.
Therefore, from the viewpoint of Manabe-Moller and Manabe-Strickler, the emphasis in this research was not on Schwarzschild's equations, but on Emden's solution. But with this shift of focus, the right-hand side of the equation, its constrained character, and the prescribed magnitude, finally disappeared.
The books an atmospheric physics and radiation brought back Schwarzshild's equations into the attention, but the climate papers went on computing temperature changes by the greenhouse gases and simulated Earth's climate through computer models, where the changes in convection were functions of the surface temperature, but not restricted by radiative transfer constraints. Manabe (971), Manabe and Wetherald (1967, 1975, 1980) are talking about climate sensitivity without mentioning the existence of the constrained character of surface net radiation.
Their followers, Ramanathan and Coakley (1978), Ramanathan et al. (1979), and The Charney Report (1979) do not refer to Schwarzshild's constraint, although at that time it was already there in Goody (1964, Mentzel (1967), Houghton (1977), Chamberlain (1978), and so on.
And finally, it it missing from all the IPCC Reports (1990-2021).
In 1991, Dr. Graeme Stephens had a huge opportunity to re-introduce Schwarzschild to the climate community. When the GEWEX project was initiated, he wrote four papers in the Earth's radiation budget and its relation to atmospheric hydrology (JGR), and in the first paper he took the equations from Mihalas (1978) and from Goody and Yung (1989), in this form:
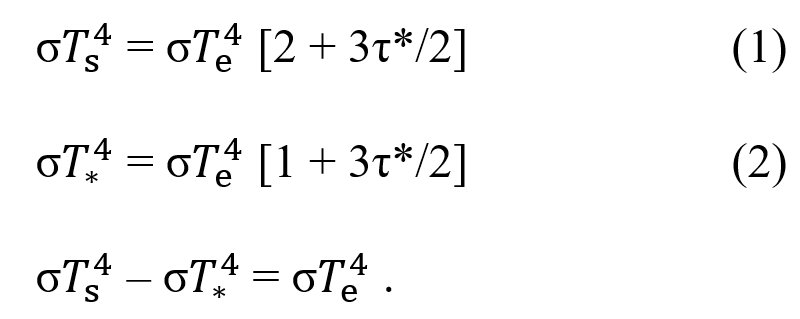
The fourth paper of the series (1994) gives the equations correctly:
Here the first equation is still the middle-term is Schwarzschild (1906, eq.11), but the second equation is not the first term (the emission of the layer), but the third term (the downward emission). So here the net radiation can be calculated correctly is F∞/2, but it is not expressed explicitly. This problem could have been avoided if he took the equations directly from Schwarzschild.
But finally, the all-sky version of this equation, together with its total-energy counterpart, is verified with a difference of 0.1 Wm-2 in the most recent, and most comprehensive study on 30 years of GEWEX, by Stephens and Coauthors (2023, BAMS).
***