A Historical Radiative Transfer Constraint on the Net Radiation at the Surface and Convection
Robert
Emden realized in 1913, that in the radiative equilibrium solution of
the Schwarzschild (1906, Eq. 11) two-stream equation, there is a jump
in temperature between the lowest atmospheric layer and the ground, of
about 20°C, but in the same sentence he noted that this jump
was
greatly diminished by heat cunduction and evaporation (this way I think
Emden discovered the concept of radiative-convective equilibrium).


Emden
does not provide us with the explicit formula from the
Schwarzschild-equation for the jump — that is, for the net radiation at
the surface and the corresponding convective fluxes — altough it is
evident from the first sight on the equation.
The first study I was able to identify from where the formula may be computed, is Ostriker (1963).

The first study I was able to identify from where the formula may be computed, is Ostriker (1963).

Here follows that the
discontinuity in temperature between the lowest atmospheric layer
and the ground is half
of the effective emission, and it does not depend on the optical depth
— as we will see in the original Schwarzschild-paper in our Part III.
It is explicit in Goody (1964), also in the second edition (1989):

It is explicit in Goody (1964), also in the second edition (1989):

And
it is shown, also explicitly, in several university textbooks on
atmospheric physics and radiation (Houghton, Chamberlain, Vaardavas and
Taylor, Visconty, Hartmann, Salby, Pierrehumbert, Andrews, Ambaum etc.):
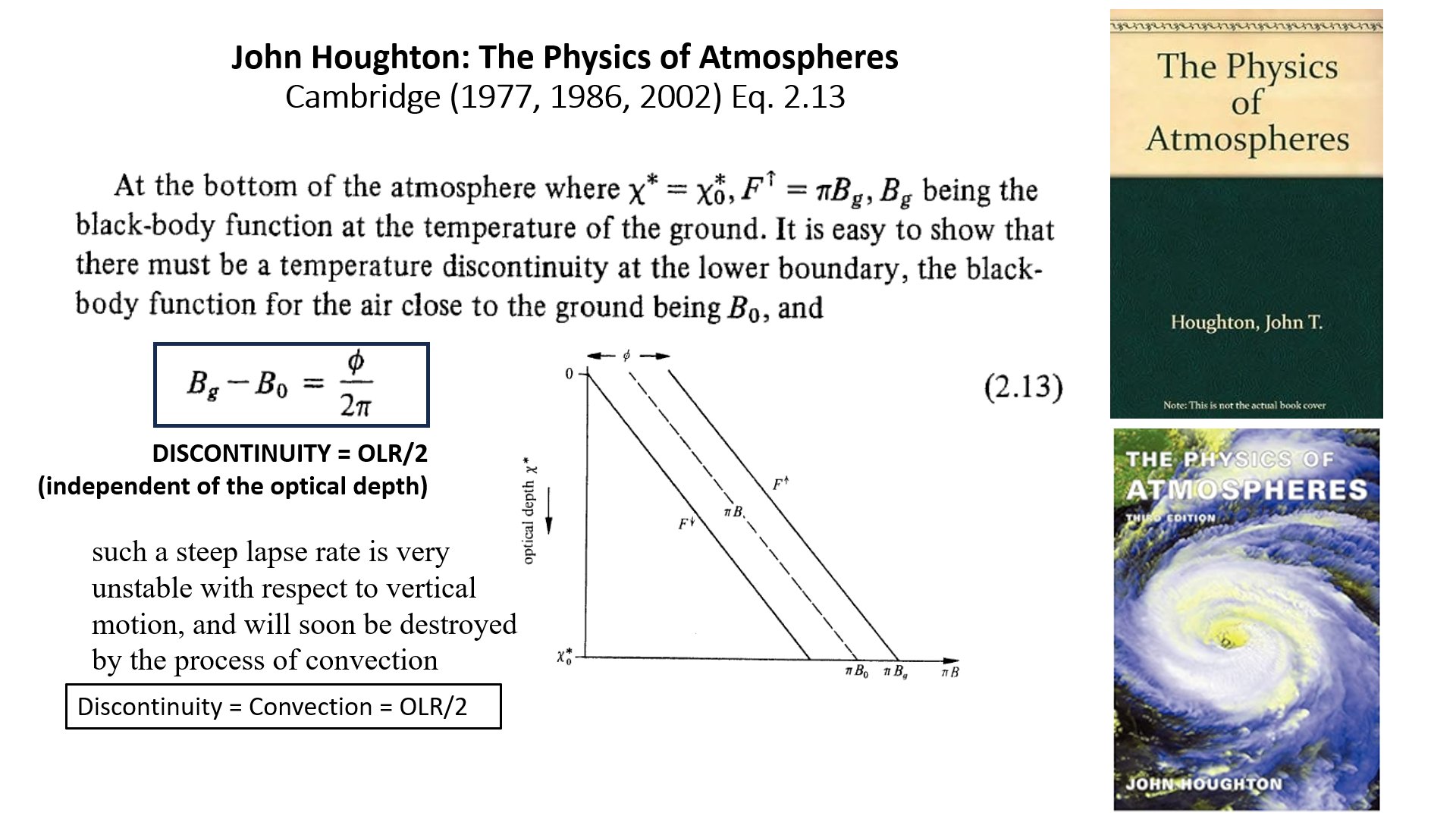
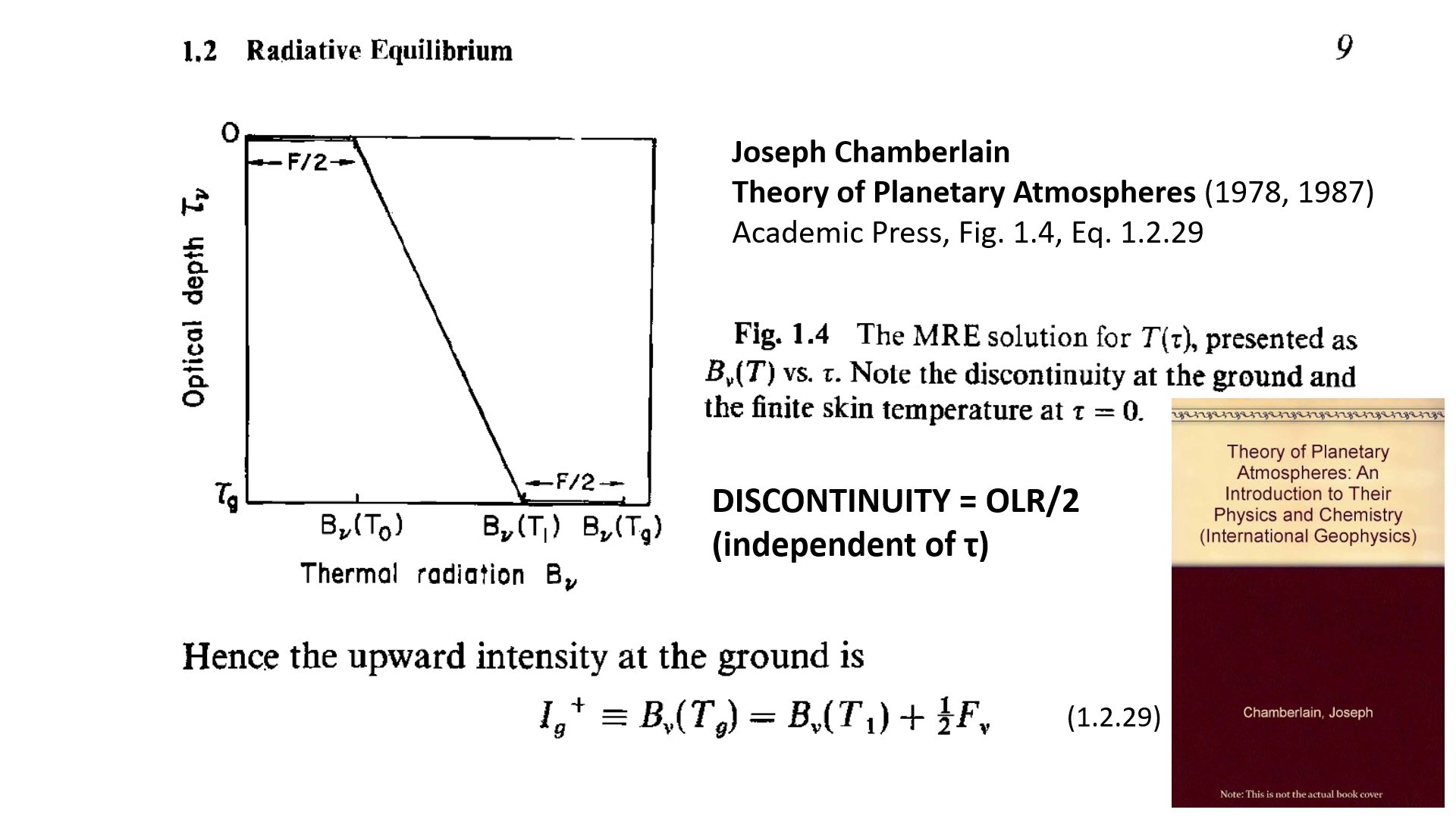



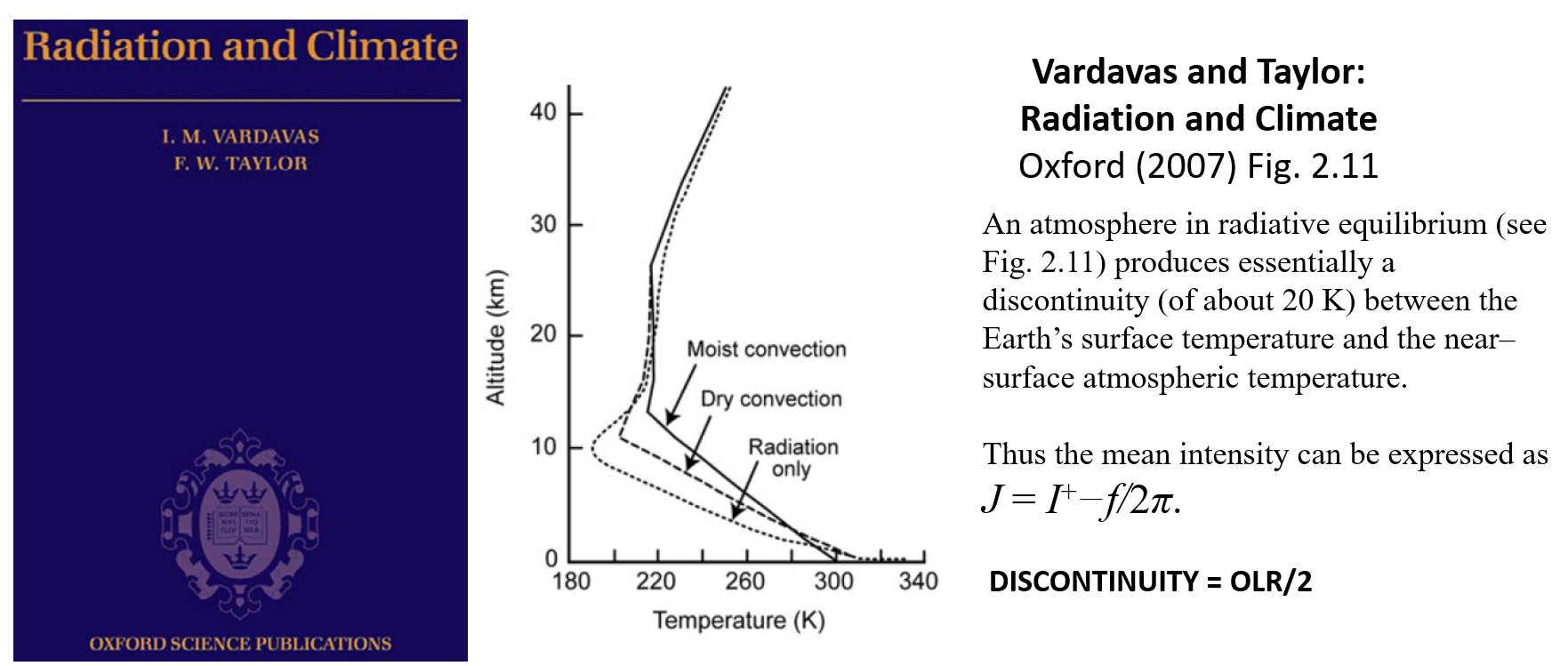

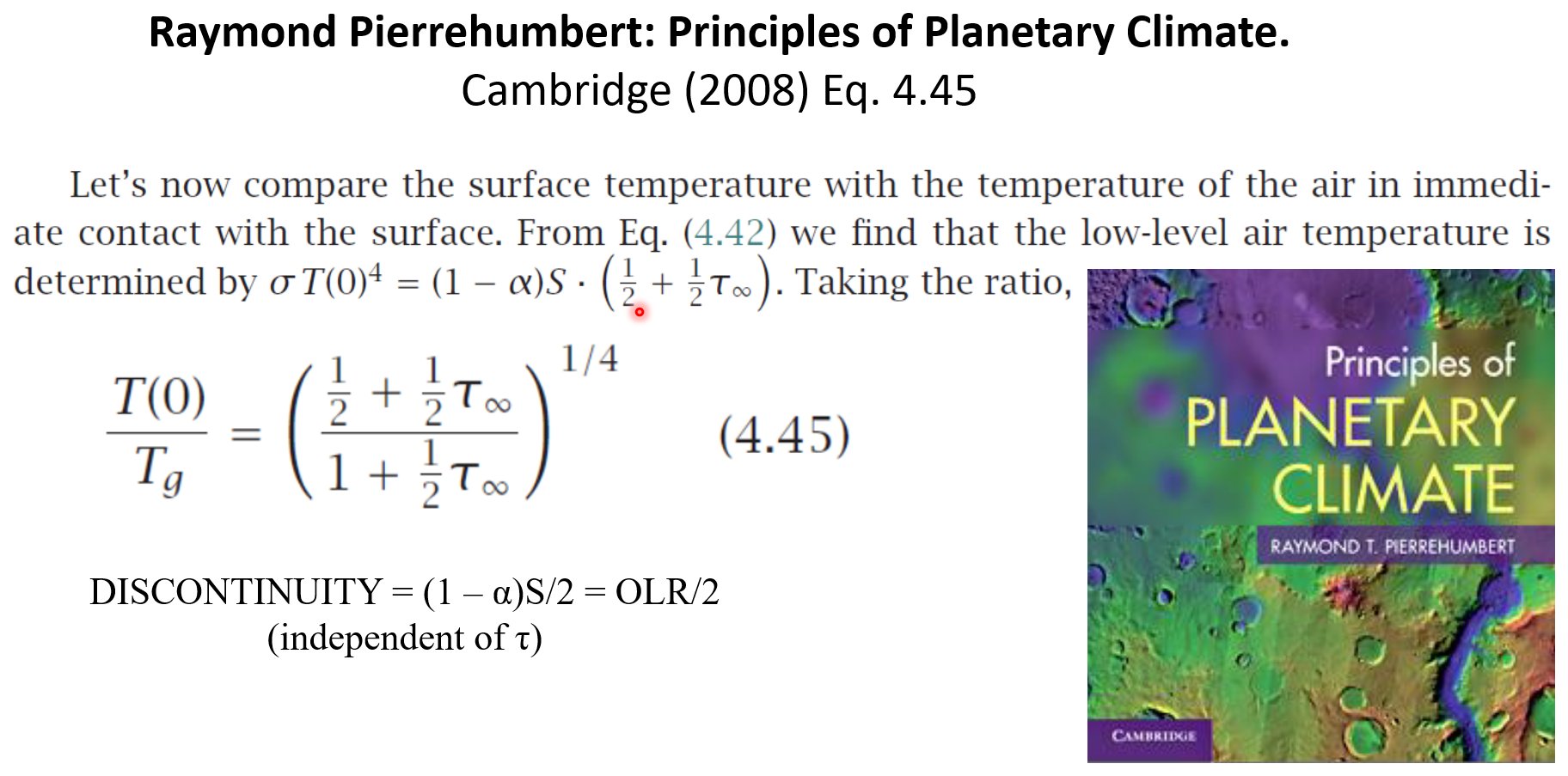
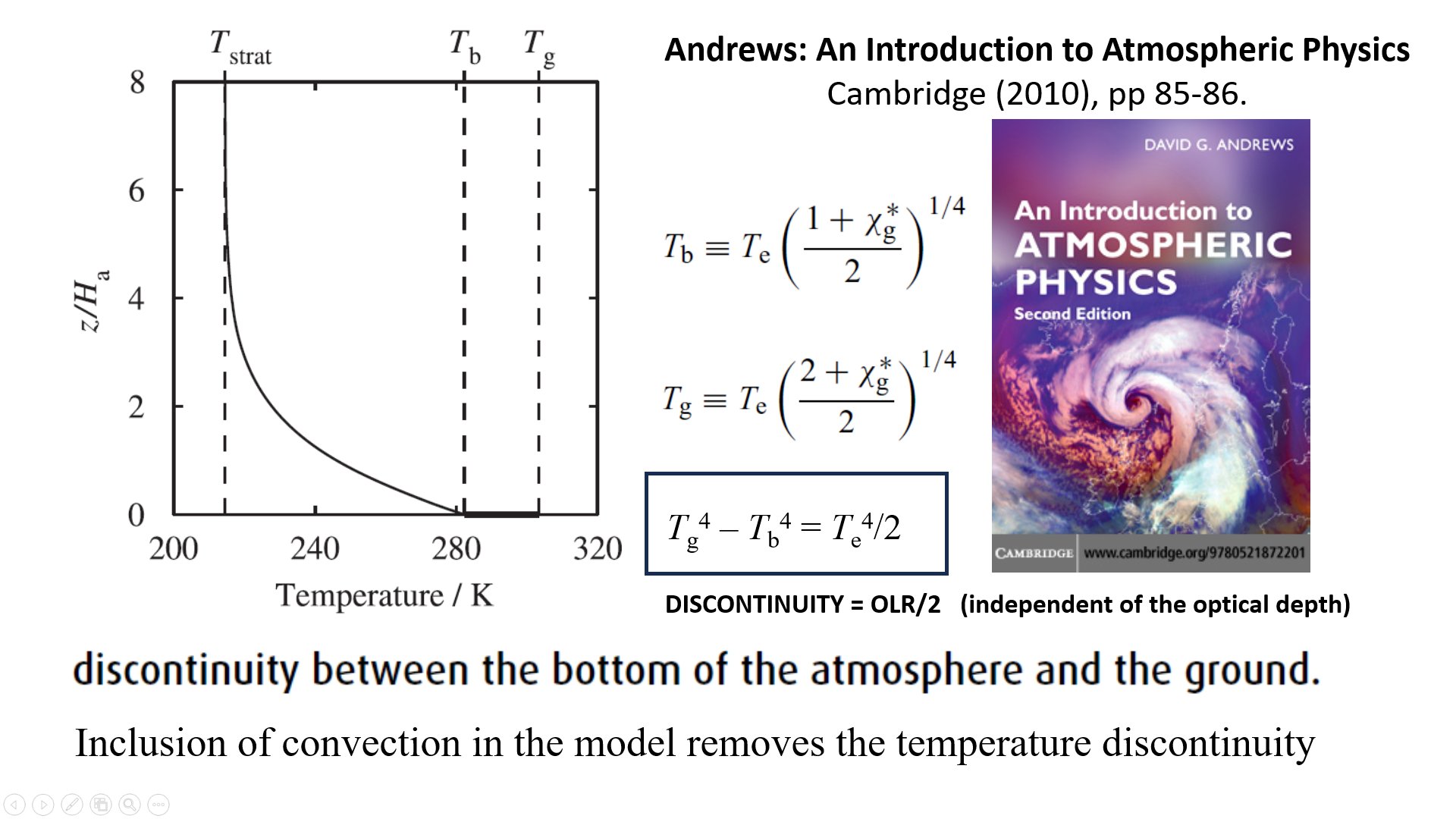
And the most recent one from the Royal Meteorological Society, 2021:
The temperature discontinuity at the surface is half of the solar radiation, removed by the turbulent heat exchange:

***
Okay, it seems as a theoretical must. But does the Earth know about it? Let's check it first on the clear-sky data of Wild (2020). Using
CIMP6 data (red): Net radiation at the surface = 215 + 318 - 400 = 133, OLR/2 = 131, the diffference is 2 Wm-2.
CIMP5 data (pink): Net radiation at the surface = 219 + 315 - 399 = 135, OLR/2 = 131.5, the diffference is 3.5 Wm-2.
Wild et al. data (black): Net radiation at the surface = 214 + 314 - 398 = 130, OLR/2 = 133.5, the diffference is -3.5 Wm-2.
Kato et al. data (green): Net radiation at the surface = 214 + 314 - 398 = 130, OLR/2 = 134, the diffference is -4 Wm-2.
Not bad, but let's see direct CERES data.
When I first encountered this equation, nine years ago, CERES EBAF Edition 2.8 was available. Taking the data from their Data Quality Summary (release date: March 27, 2015), and the data covered ten years from March 2000 through February 2010, we find:
Surface Net = Surface SW net + LW net =
Surface (SW down - SW up + LW down - LW up) (clear-sky) = OLR(clear-sky) /2
243.9 - 29.7 + 316.0 - 398.0 = 265.7/2 - 0.6 Wm-2.
The difference is again 0.6 Wm-2 only, the same as TOA imbalance at that time.
Let me use this to support my choice in the deduction point (iv), where I took CONV = OLR/2.
This decision is further supported by the new, improved Edition 4.1 clear-sky data (April 2000 - March 2022):
240.87 - 29.10 + 317.40 - 398.52 = 266.01 - 2.35 Wm-2.
No its time to introduce the all-sky version for this equation. Here we need to separate atmospheric transfer of radiation from the longwave cloud radiative effect, therefore, after using all-sky data both at the left-hand side and in OLR at the right-hand side, LWCRE should be subtracted; then comes the division by two:
Surface (SW down - SW up + LW down - LW up) (all-sky) = [OLR(all-sky) - LWCRE]/2
186.85 - 23.16 + 345.01 - 398.75 = (240.25 - 25.77)/2 + 2.71 Wm-2.
It is known from Loeb et al. (2009) that there is a 2.5 Wm-2 TOA flux adjusment in the LW; the mean bias of this pair of clear-sky and all-sky net equations is 0.18 Wm-2; very convincing.
That's why in step (xii), all-sky deduction, CONV = 4 is the correct choice with OLR(all) = 9 and LWCRE = 1, since the all-sky equation for the net radiation at the surface looks like this: 4 = (9 - 1)/2.
Since in radiative-convective equilibrium RN, the net radiation at the surface equals the convective flux, that is sensible heat plus latent heat, we may readily control the equation on the published global energy flow diagrams.
Let's try the latest one, based on 30 years of GEWEX research (Stephens et al., 2023, BAMS)
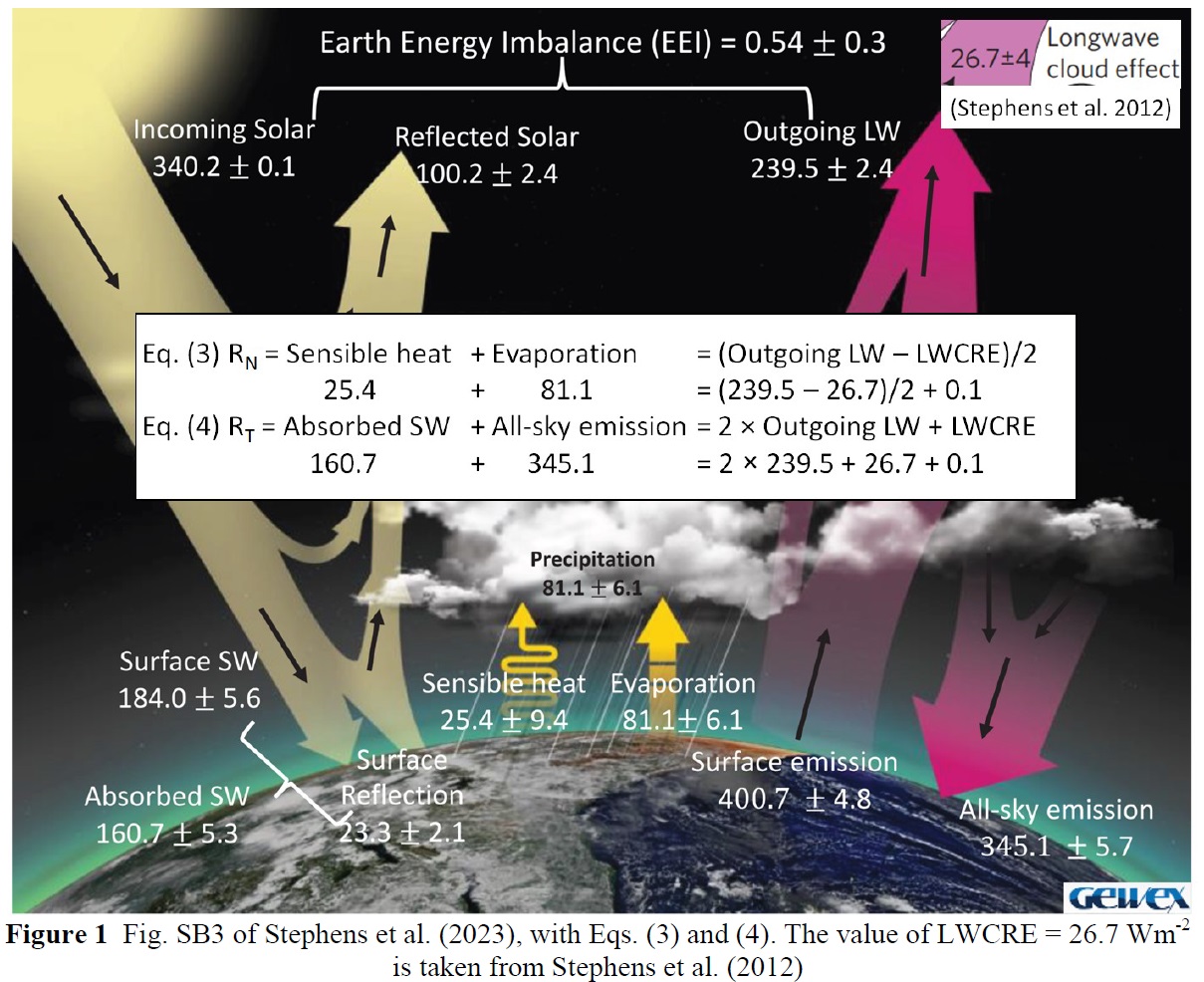
Since clear-sky OLR or LWCRE is not given here, I took it from an earlier paper of the same authors (Stephens et al. 2012Ö as LWCRE = 26.7 Wm-2. With this, the all-sky net equation is satisfied by the data of the diagram by a difference of 0.1 Wm-2.
***
I mentioned several constraints in the deduced geometric integer ratio systems. An evident, conspicuous relation is that the 1: 2 : 1 ratio of the original starting point, the simplest geometric model is conserved and maintained in the final structure of the clear-sky energy flows.
The total radiation at the surface, RT, that is the absorbed solar plus the absorbed longwave, is equal to 2OLR:
RT = Surface (SW absorbed + LW absorbed) (clear-sky) = 2OLR(clear-sky),
8 + 12 = 2 × 10
in the clear-sky integer system,
and, in the all-sky, since LWCRE is included in the left-hand side in DLR, it must be added to the right-hand side as well:
RT = Surface (SW absorbed + LW absorbed) (all-sky) = 2OLR(all-sky) + LWCRE.
6 + 13 = 2 × 9 + 1
in the all-sky integer system.
The accuracy of constraint on total radiation at the surface, with the data in the GEWEX diagram, is again 0.1 Wm-2.
***
PART IV
THE EQUATIONS









And the most recent one from the Royal Meteorological Society, 2021:
The temperature discontinuity at the surface is half of the solar radiation, removed by the turbulent heat exchange:

***
Okay, it seems as a theoretical must. But does the Earth know about it? Let's check it first on the clear-sky data of Wild (2020). Using
CIMP6 data (red): Net radiation at the surface = 215 + 318 - 400 = 133, OLR/2 = 131, the diffference is 2 Wm-2.
CIMP5 data (pink): Net radiation at the surface = 219 + 315 - 399 = 135, OLR/2 = 131.5, the diffference is 3.5 Wm-2.
Wild et al. data (black): Net radiation at the surface = 214 + 314 - 398 = 130, OLR/2 = 133.5, the diffference is -3.5 Wm-2.
Kato et al. data (green): Net radiation at the surface = 214 + 314 - 398 = 130, OLR/2 = 134, the diffference is -4 Wm-2.
Not bad, but let's see direct CERES data.
When I first encountered this equation, nine years ago, CERES EBAF Edition 2.8 was available. Taking the data from their Data Quality Summary (release date: March 27, 2015), and the data covered ten years from March 2000 through February 2010, we find:
Surface Net = Surface SW net + LW net =
Surface (SW down - SW up + LW down - LW up) (clear-sky) = OLR(clear-sky) /2
243.9 - 29.7 + 316.0 - 398.0 = 265.7/2 - 0.6 Wm-2.
The difference is again 0.6 Wm-2 only, the same as TOA imbalance at that time.
Let me use this to support my choice in the deduction point (iv), where I took CONV = OLR/2.
This decision is further supported by the new, improved Edition 4.1 clear-sky data (April 2000 - March 2022):
240.87 - 29.10 + 317.40 - 398.52 = 266.01 - 2.35 Wm-2.
No its time to introduce the all-sky version for this equation. Here we need to separate atmospheric transfer of radiation from the longwave cloud radiative effect, therefore, after using all-sky data both at the left-hand side and in OLR at the right-hand side, LWCRE should be subtracted; then comes the division by two:
Surface (SW down - SW up + LW down - LW up) (all-sky) = [OLR(all-sky) - LWCRE]/2
186.85 - 23.16 + 345.01 - 398.75 = (240.25 - 25.77)/2 + 2.71 Wm-2.
It is known from Loeb et al. (2009) that there is a 2.5 Wm-2 TOA flux adjusment in the LW; the mean bias of this pair of clear-sky and all-sky net equations is 0.18 Wm-2; very convincing.
That's why in step (xii), all-sky deduction, CONV = 4 is the correct choice with OLR(all) = 9 and LWCRE = 1, since the all-sky equation for the net radiation at the surface looks like this: 4 = (9 - 1)/2.
Since in radiative-convective equilibrium RN, the net radiation at the surface equals the convective flux, that is sensible heat plus latent heat, we may readily control the equation on the published global energy flow diagrams.
Let's try the latest one, based on 30 years of GEWEX research (Stephens et al., 2023, BAMS)

Since clear-sky OLR or LWCRE is not given here, I took it from an earlier paper of the same authors (Stephens et al. 2012Ö as LWCRE = 26.7 Wm-2. With this, the all-sky net equation is satisfied by the data of the diagram by a difference of 0.1 Wm-2.
***
I mentioned several constraints in the deduced geometric integer ratio systems. An evident, conspicuous relation is that the 1: 2 : 1 ratio of the original starting point, the simplest geometric model is conserved and maintained in the final structure of the clear-sky energy flows.
The total radiation at the surface, RT, that is the absorbed solar plus the absorbed longwave, is equal to 2OLR:
RT = Surface (SW absorbed + LW absorbed) (clear-sky) = 2OLR(clear-sky),
8 + 12 = 2 × 10
in the clear-sky integer system,
and, in the all-sky, since LWCRE is included in the left-hand side in DLR, it must be added to the right-hand side as well:
RT = Surface (SW absorbed + LW absorbed) (all-sky) = 2OLR(all-sky) + LWCRE.
6 + 13 = 2 × 9 + 1
in the all-sky integer system.
The accuracy of constraint on total radiation at the surface, with the data in the GEWEX diagram, is again 0.1 Wm-2.
***
PART IV
THE EQUATIONS