Geometric Deduction
The
starting point of the deduction is the simplest greenhouse model,
consisting og a surface
and a solar-transparent, infrared-opaque
atmospheric layer — as for example is shown in Hartmann (1994), Global
Physical
Climatology, Fig. 2.3:
![]()
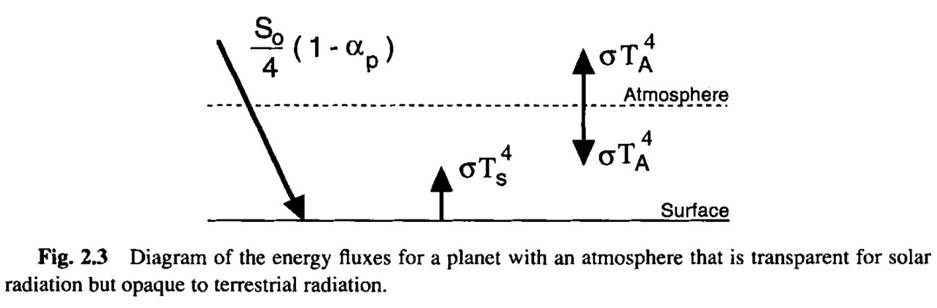
***
GEOMETRIC
DEDUCTION
(i) Starting point: The simplest
greenhouse model.
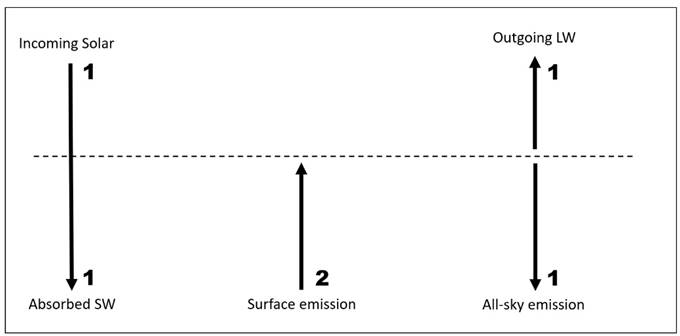
***
(ii)
Multiply the unit by five.
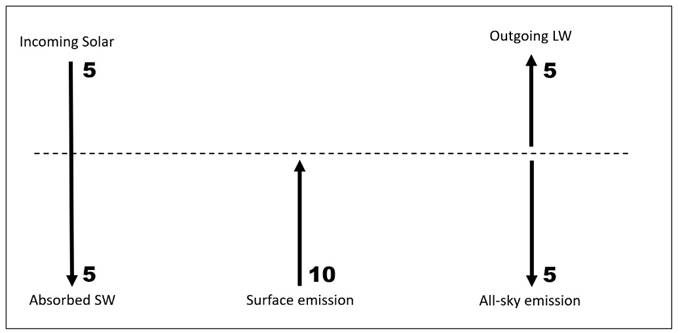
***
(iii)
Allow one unit for reflected solar at the top of the atmosphere.
Absorbed solar
and outgoing LW decrease to four units, surface upward LW emission
decreases to
eight units, and all-sky (downward) atmospheric emission to the surface
decreases to four units.
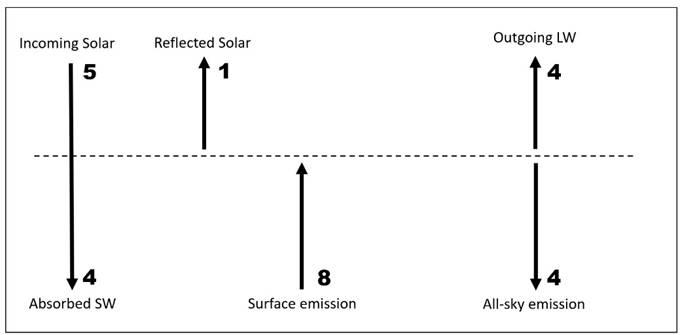
***
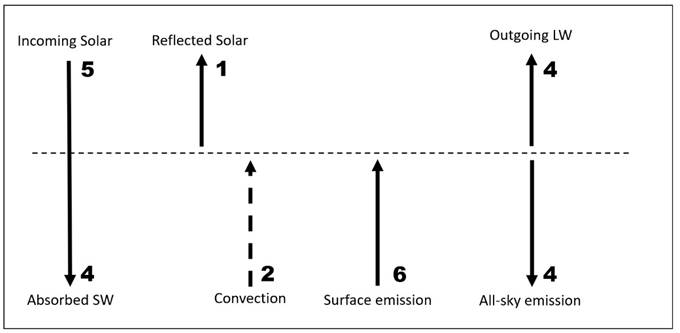
(iv)
Introduce two units for convection. Surface emission decreases to six
units.
***
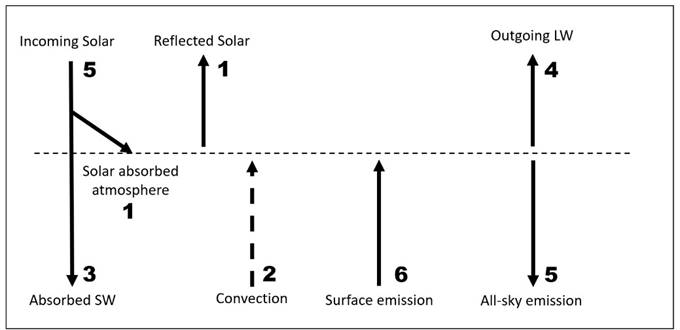
(v) Allow
one unit for solar absorption in the atmosphere. Surface SW absorption
decreases to three units, all-sky emission downward increases to five
units.
***
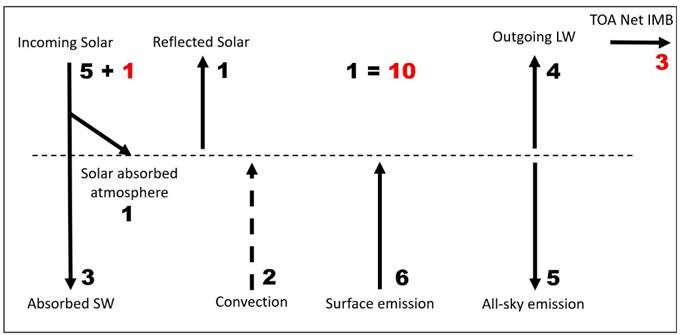
(vi) Fine
tuning: let be one black unit = ten red units; add one red unit to
Incoming solar;
and allow three red units as clear-sky TOA imbalance. This
way, 2 red
unit hiatus was generated at TOA.
***
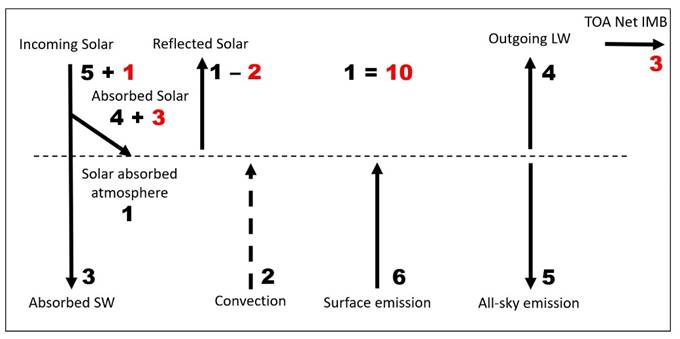
(vii)
Solution: reflect two red units les, thus absorb three red
units more.
***
(viii)
Re-distribute the absorbed three plus red units as add one red unit to
solar
absorbed atmosphere and two units to SW absorbed surface. All-sky
downward
emission decreases by two red units.
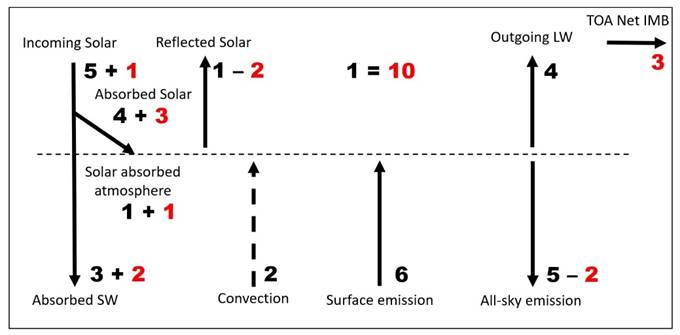
Ready.
This is the geometric deduction of the clear-sky system on
the intercepting
cross-section disk to incoming solar radiation (before division by 4
for
spherical weighting).
(ix) Now
transform into red units:
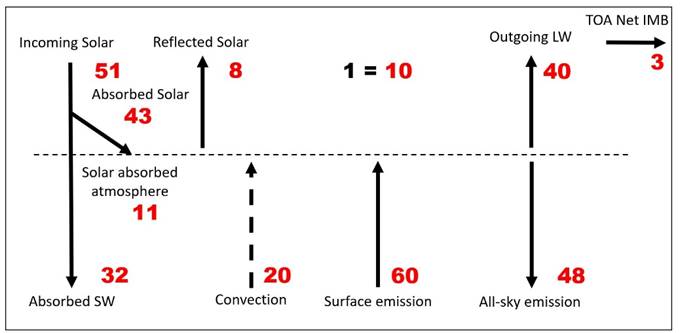
(x) Divide
by four for spherical weighting and show the theoretical values
using 1 unit = 26.68 Wm-2:
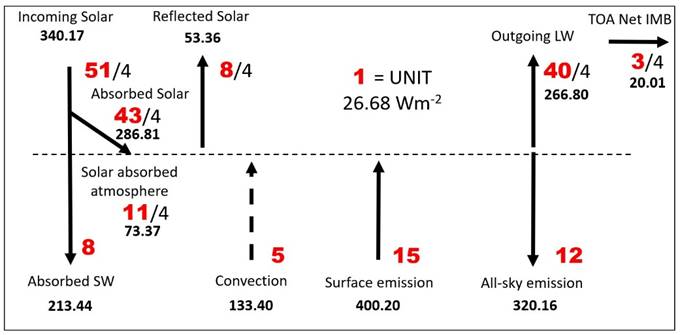
(xi) Put
in observed / modeled best estimate clear-sky values from Wild
(2020):
THE
CLEAR-SKY SYSTEM
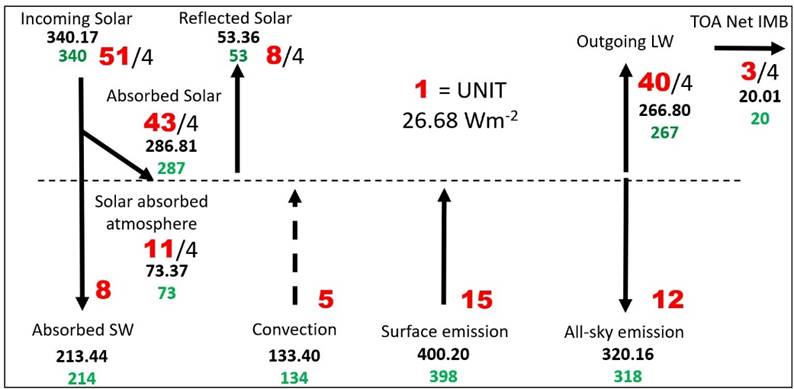
(xii)
Finally, we create the all-sky system, by decreasing clear-sky
OLR
from 10 units to 9 units and
increasing downward longwave
all-sky emission of the atmosphere to the surface
from 12 units
to 13 units; and showing the best all-sky data from
Wild (2020):
ALL-SKY
SYSTEM
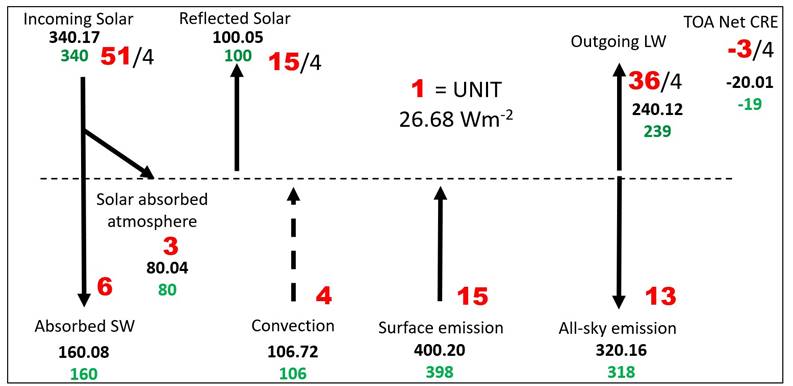
These
definite structures evidently contain several built-in constraints.
Some of
them were know already previously, but somehow got forgotten. In the
next part
we show that the step in (iv), where convection was introduced in the
clear-sky
(as exactly one-half of Outgoing LW, and three-halves of surface upward
emission), depends on a well-known and long-known theoretical radiation
transfer constraint relationship, which is widely described in
university
textbooks on atmospheric radiation, but missing from the climate
discussions in
journal articles.
PART THREE
Further
details:
Zagoni,
M.: Trenberth’s (2022) Greenhouse Geometry, EGU General Assembly 2024,
Vienna,
Austria, 14–19 Apr 2024, EGU24-7
https://doi.org/10.5194/egusphere-egu24-7
Supplementary
Material (video) (1:31:58):
https://www.earthenergyflows.com/Zagoni-EGU2024-Trenberths-Greenhouse-Geometry_Full-v03-480.mp4