Earth’s
Global Energy Budget
by
Miklos Zagoni
email:
miklos.zagoni@t-online.hu
This website offers talks, abstracts and presentations given in the past four years at NASA Langley,
AGU, EGU, Gewex, Am Met Soc, IUGG and CLIVAR conferences and forthcoming meetings.
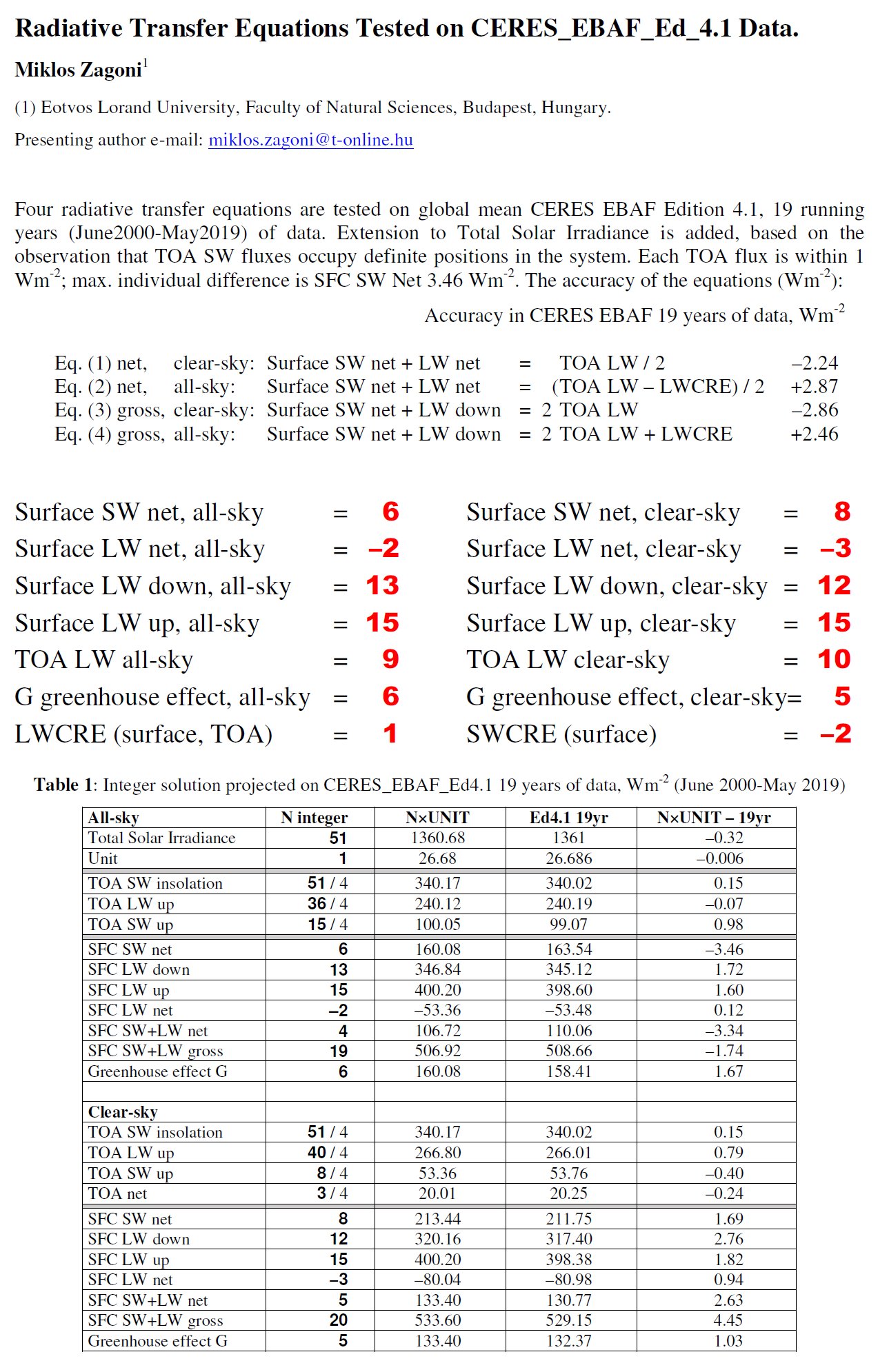
Earth's annual global mean fluxes can be deduced from four equations,
from which the first is long known as approximation to Schwarzschild's radiative transfer equation;
the other three are its all-sky and 'gross' extensions.
These equations, together, define a theoretical value for the greenhouse effect (related to OLR),
which belongs to the model only and does not refer to the atmospheric composition.
This value can be compared to real surface and satellite observations and proved to be equal
to the observed value far within the measurement uncertainty.
* * *
*
*
* * *
*
*
* * *
A planned talk at the 33rd CERES Science Team Meeting:
***
***
* * *
EGU 2020 Abstract (accepted):
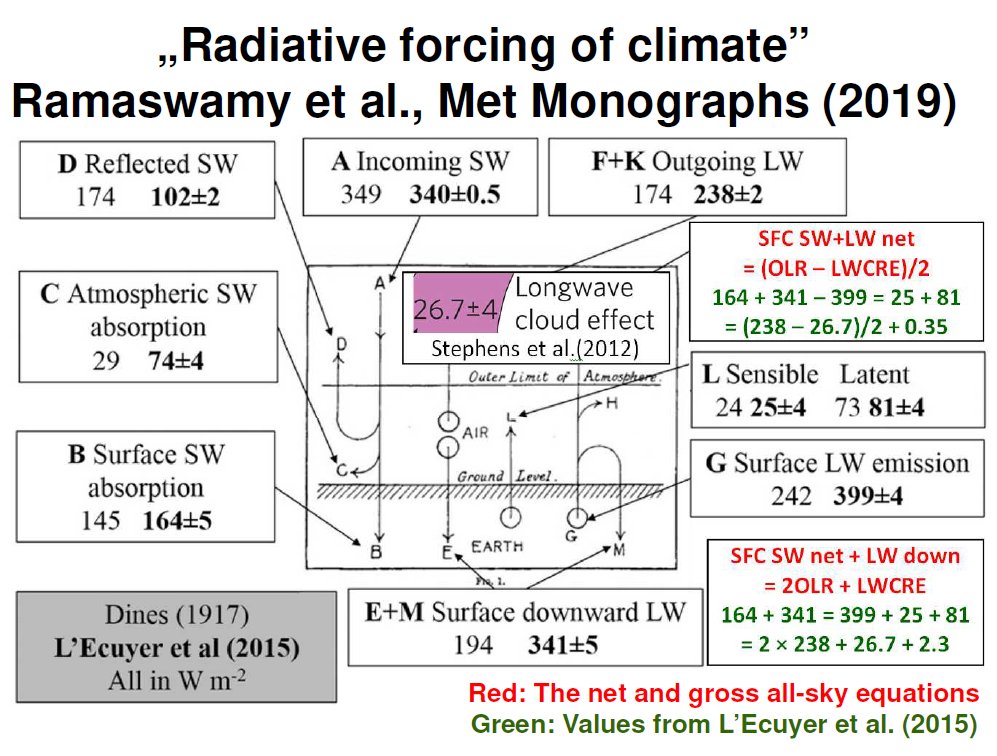
The WCRP Coupled Model Intercomparison Project (CMIP) simulations expect increasing downward longwave radiation (DLR, surface LW down) from a human-enhanced greenhouse effect during the 21st century in the range of 10 – 40 Wm-2. We announce a public challenge to these predictions based on a long known but rarely referred theoretical constraint. Following the logic of original radiative transfer equations of Schwarzschild (1906, Eq. 11), a relationship connects surface net radiation to the effective emission, independent of the optical depth. This relationship is reproduced by several textbooks on atmospheric radiation like Goody (1964, Eq. 2.115), Goody and Yung (1989, Eq. 2.146), Houghton (2002, Eq. 2.13), Pierrehumbert (2010, Eq. 4.44-4.45). In CERES notation: Surface [shortwave (SW) + longwave (LW)] net = OLR/2. A specific “gross” version is: Surface (SW net + LW down) = 2OLR. These are for the cloudless case. Their all-sky form includes longwave cloud radiative effect (LWCRE): Surface SW+LW net = (OLR – LWCRE)/2 and Surface (SW net + LW down) = 2OLR + LWCRE. Controlling these four equations on CERES EBAF Edition 4.1, 18 years of data, and on EBAF Ed4.1 Data Quality Summary Table 2-1 and Table 4-1, each of them is valid within 3 Wm-2. The all-sky versions are satisfied by the IPCC-AR5 (2013) global energy budget (Fig. 2.11) and a water cycle assessment (Stephens and L'Ecuyer 2015) within 2 Wm-2. We couldn't find any reference to these equalities in the literature on general circulation models or climate sensitivity. Applying known definitions, the equations can be solved for LWCRE, resulting in a set of small integers (Zagoni, EGU2019). All-sky fluxes: Surface SW net = 6; Surface LW net = –2; DLR = 13; OLR = 9. Clear-sky fluxes: Surface SW net = 8; Surface LW net = –3; DLR = 12; OLR = 10; Surface LW up (ULW) = 15 (both for all-sky and clear-sky); LWCRE (surface and TOA) = 1. From this solution it comes for all-sky: DLR = (13/9)OLR, ULW = (15/9)OLR, and for clear-sky ULW = (15/10)OLR. Since the physical principles and conditions behind these equations are solid and justified by observations, we expect them to remain valid in the forthcoming decades as well. CMIP6 models might represent regional distribution changes and cloud feedbacks correctly, in lack of global constraints they may lead to profoundly different outcomes in the long run. This is a testable difference. To check the robustness and stationarity of our equations, we challenge published CMIP5 predictions. We predict for the 21st century: all-sky DLR = (13/9)OLR ± 3.0 Wm-2; ULW = (15/9)OLR ± 3.0 Wm-2 and clear-sky ULW = (15/10)OLR ± 3.0 Wm-2. Initial status (CERES EBAF Edition 4.1 annual global means for 2018): all-sky OLR = 240.14, DLR = 344.82, ULW = 399.37, hence all-sky DLR = (13/9)OLR – 2.05 and ULW = (15/9)OLR – 0.86 (Wm-2); clear-sky ULW = 399.05, OLR = 265.80, hence ULW = (15/10)OLR + 0.35 Wm-2. Greenhouse effect: g(theory) = G/ULW = (ULW – OLR)/ULW = (15 – 9)/15 = 0.4, g(observed) = 0.399.
***
* * *
EGU 2020 Abstract (jpg):
* * *
EGU 2020 poster (draft):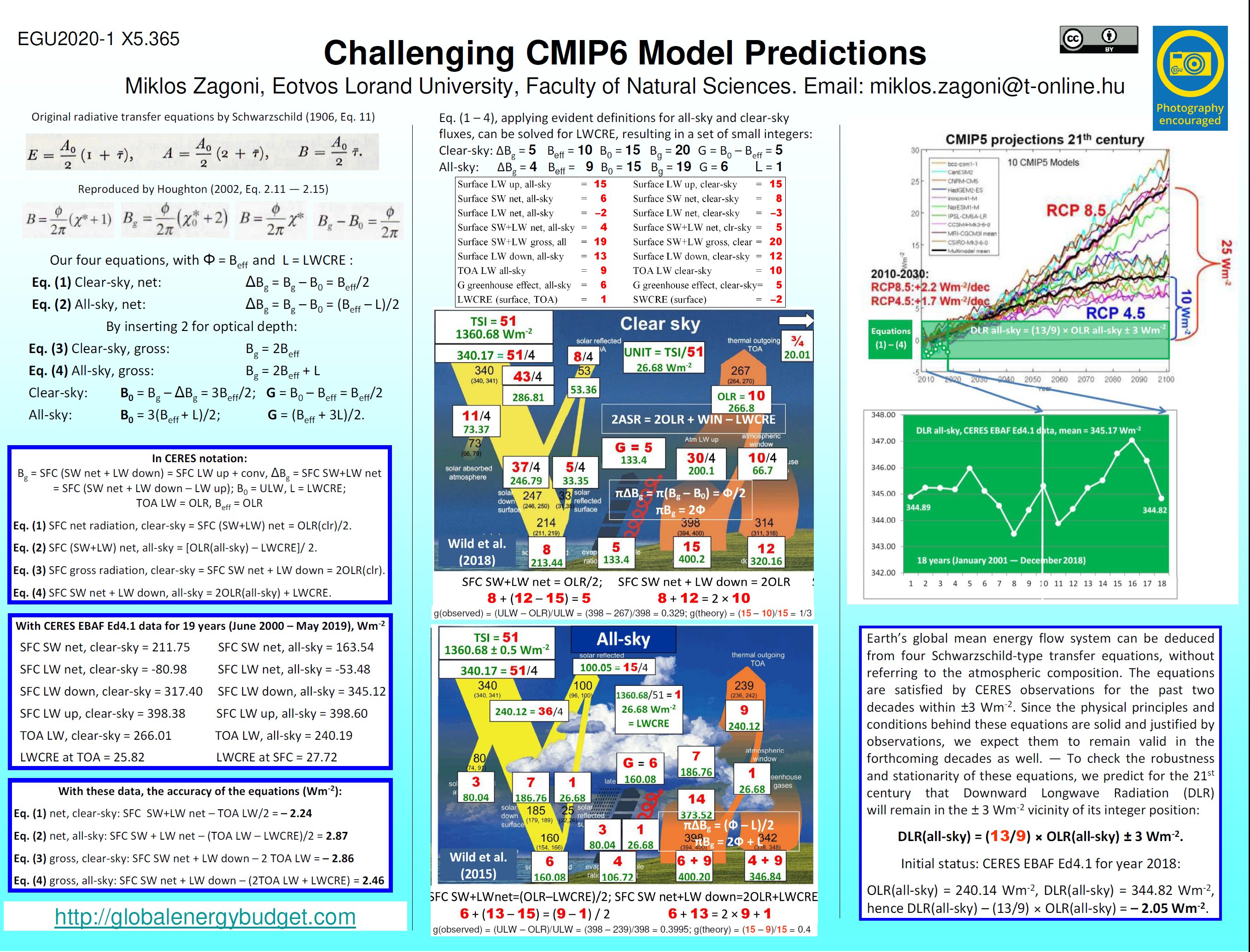
* * *
EGU 2019 Abstract (jpg):
Available at https://meetingorganizer.copernicus.org/EGU2019/EGU2019-3-4.pdf
* * *
Abstract accepted at the International Radiation Symposium IRS 2020
Thessaloniki, Greece:
* * *
Another submission:
* * *
Further details:
The net equations (Eq. 1 and 2) are independent of the optical depth by definition.
The gross equations (Eq. 3 and 4) are taken at tau = 2 (the infrared-opaque limit),
where Bg = 2Be.
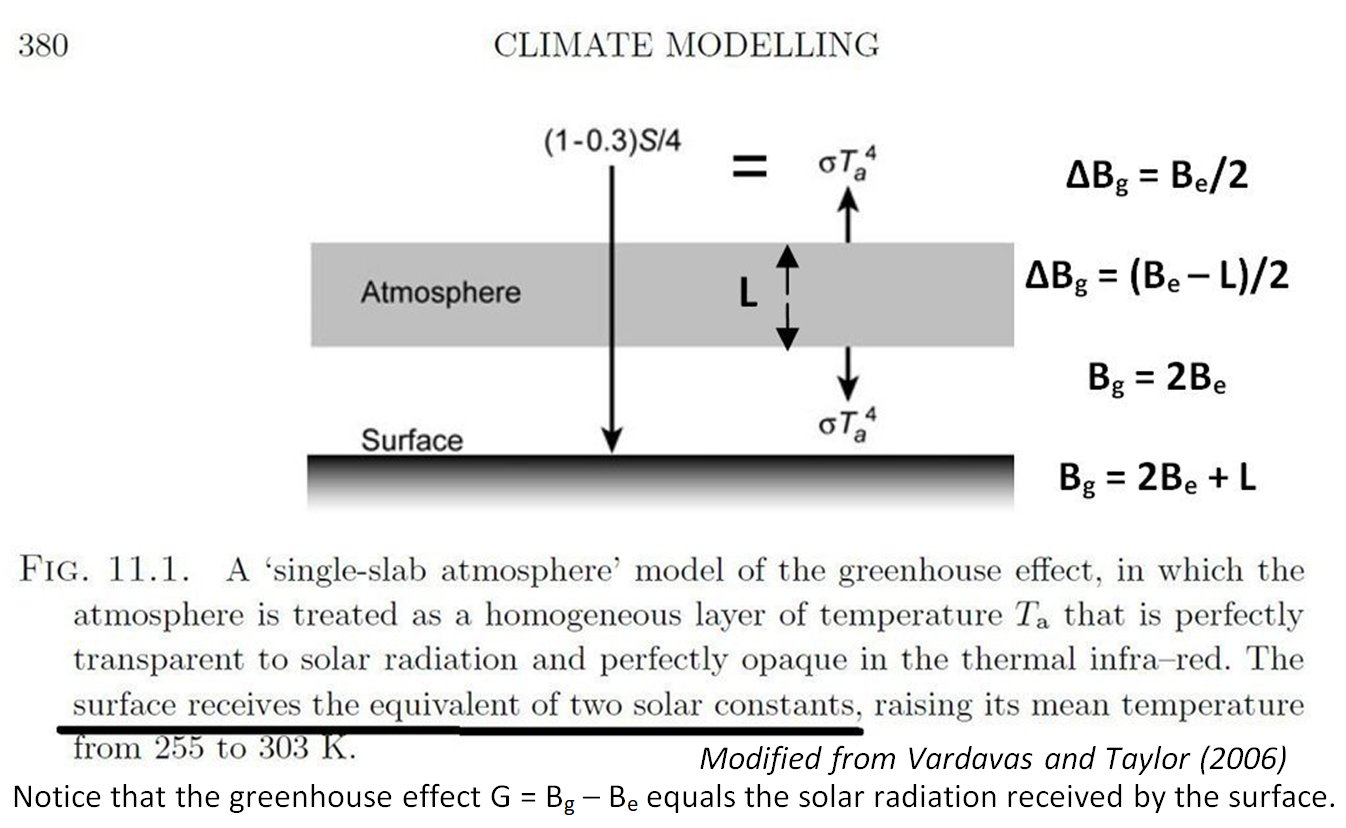
* * *

More info:
* * *
* * *
* * *
***
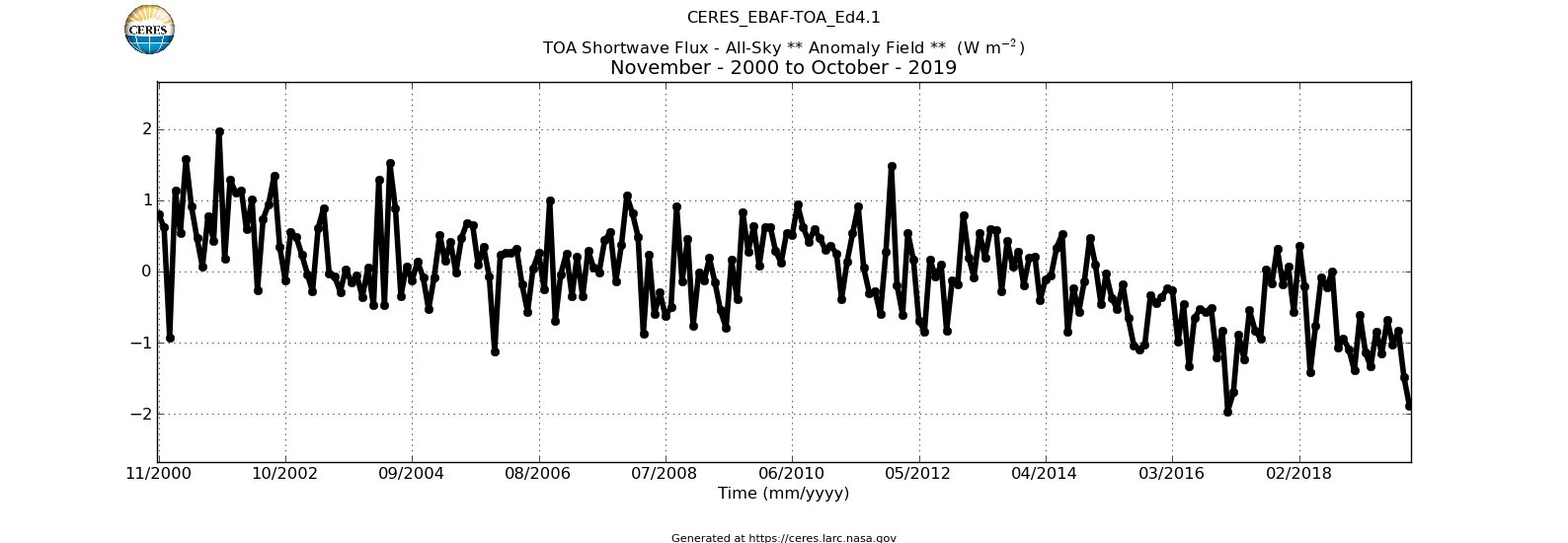
CERES observations:
TOA reflected shortwave, 19 years
***
Spring 2019 CERES Science Team Meeting (NASA LaRC, Hampton)
Spring 2018 CERES Science Team Meeting (NASA LaRC, Hampton)
Fall 2017 CERES Science Team Meeting (NASA GSFC, Washington)
AGU 2018 Fall Meeting (Washington) (draft)
Posters:
EGU 2019 General Assembly (Vienna)
2018 CLIVAR WCRP Workshop: Earth Energy Imbalance (Toulouse)
GEWEX 8th Open Science Conference 2018 (Canmore) Poster 1 / Poster 2
EGU 2018 General Assembly (Vienna) Poster 1 / Poster 2
2018 American Meteorological Society 15th Conference on Cloud Physics/
15th Conference on Atmospheric Radiation (Vancouver)
AGU 2017 Fall Meeting (New Orleans)
***
Another talk