QCD — Quantum Climate Dynamics
Contrary
to this loud title, I got only some very elementary thought fractions,
incomplete considerations, broken logical chains. But let me try.
Let's take a small prime number: let it be 17. This will be my Total Solar Irradiance, TSI = 17 units.
Let us allow 5 to be reflected. This way, we have a planetary albedo of 5/17, which is arithmetically identical to the value given by the IPCC AR6 diagram, where the all-sky TOA incoming solar radiation is 340, and the solar reflection is 100 Wm-2, hence their albedo is 100/340 = 5/17.
Another benefit is that the absorbed solar radiation is then 12 units, which, after spherical weigting (division by 4), results in 3 units absorbed solar and emitted LW radiation. Using the well-kown 1 : 2 : 1 model of the simplest greenhouse geometry in a solar-transparent and infrared-opaque atmosphere, we then have 3 uni ts solar absorbed surface, 6 units LW emitted upward by the surface, and again 3 units emitted LW downward by the atmosphere. Then introduce 1 unit of evaporation at the surfacen by decreasing upward longwave to 5 units.
I assign 80.04 Wm-2 to this 1 unit since I know in advance that it will become 3 units soon, with 1 unit = 26.68 Wm-2.
This structure is very similar to what we really have. TSI = 17 × 80.04 = 1360.68 Wm-2, while the most accurate value of TSI, according to Kopp and Lean (2011) is 1360.8 ± 0.5 Wm-2. The planetary emissivity is TOA LW / Surface ULW = 3/5 here, while in the IPCC AR6 Fig. 7.2 diagram it is 239/398 = 0.6005:
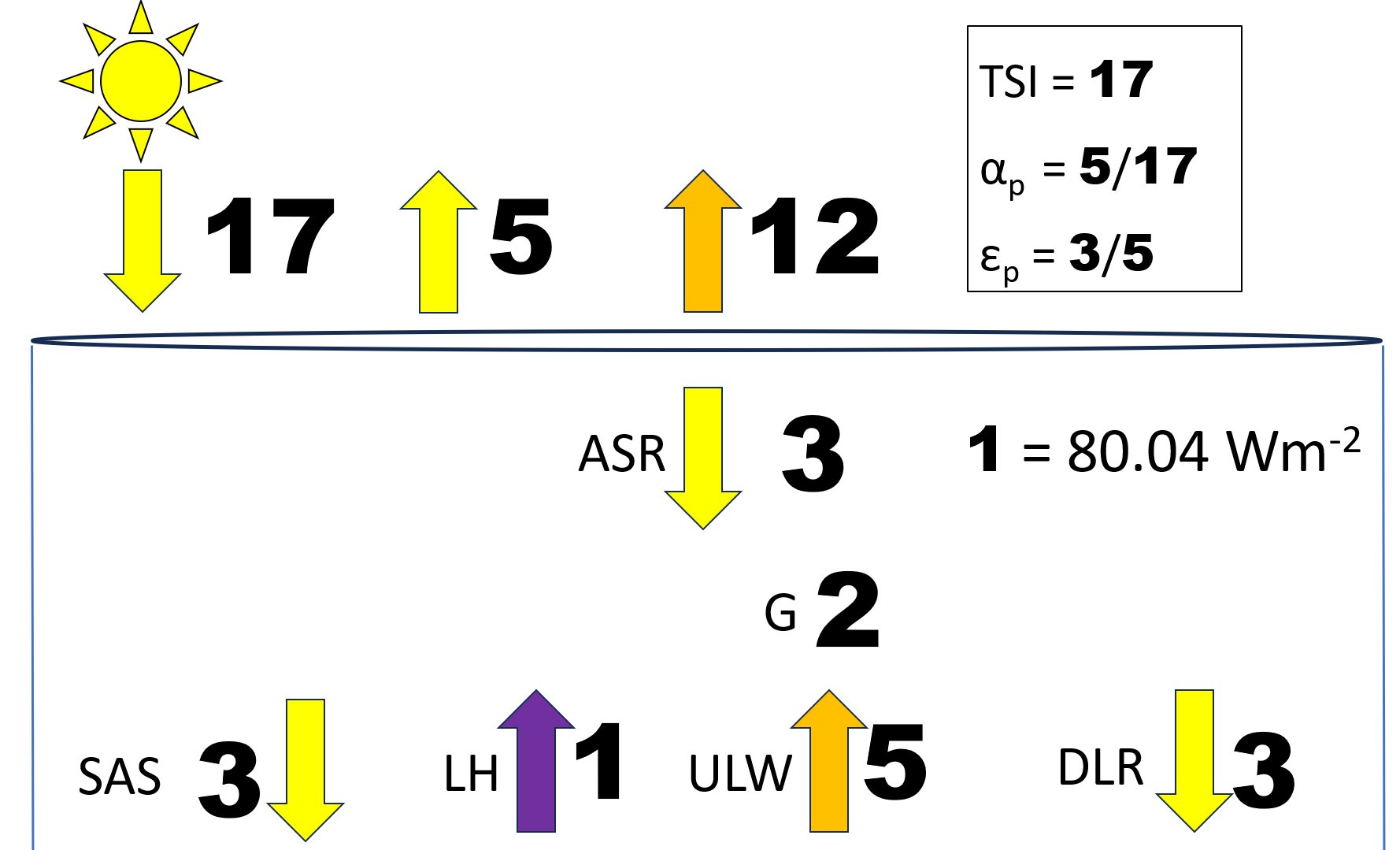
Now introduce 1 unit for solar absorbed by the atmosphere, therefore SAS decreases to 2 units, but DLR increases to 4 units:
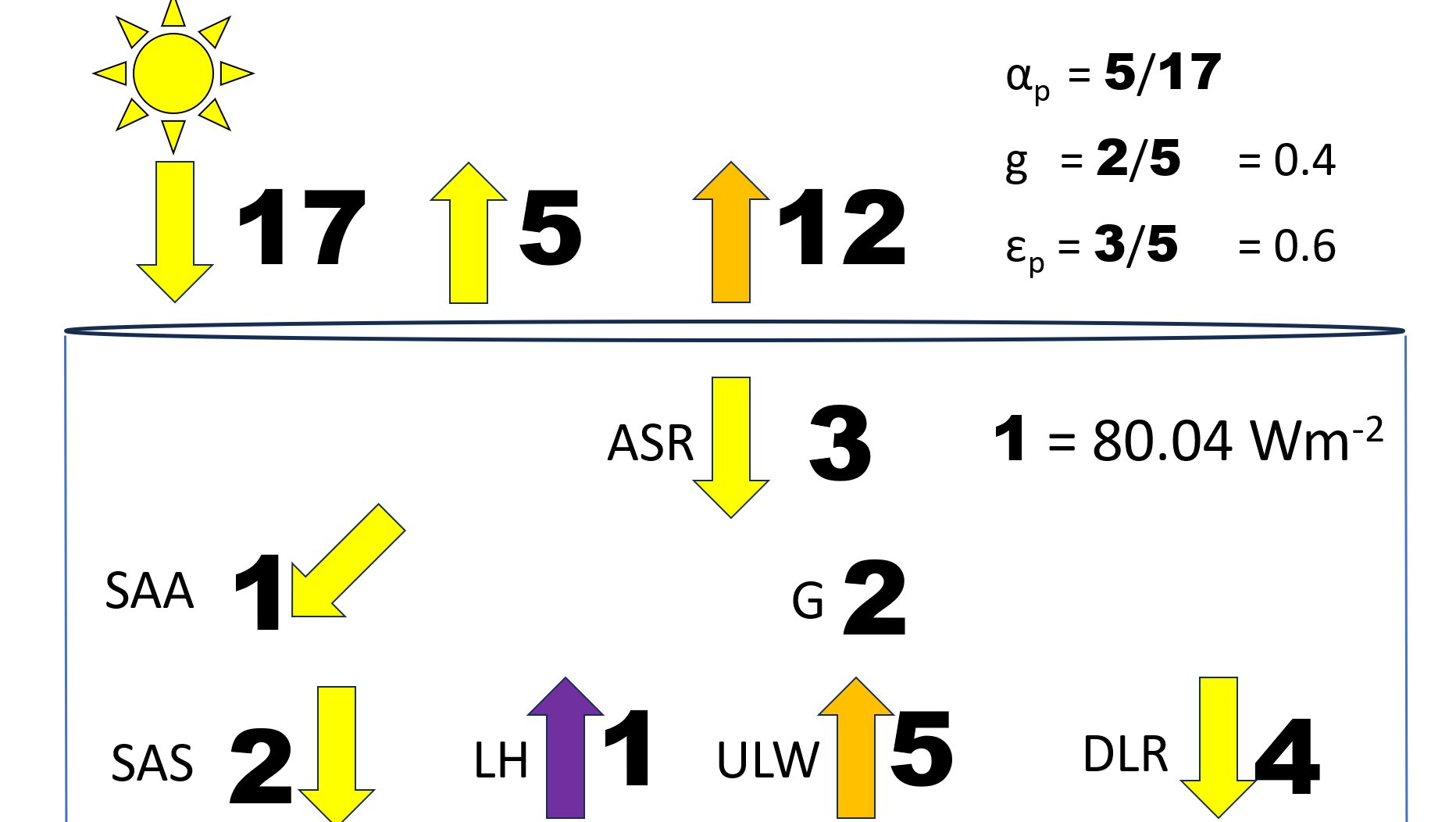
Using the 'light-wieghted' quantum of 3 = 1, let me add 1 unit to DLR (since we are in the all-sky) as LWCRE, and to balance it by 1 unit added to convection as sensible heat:
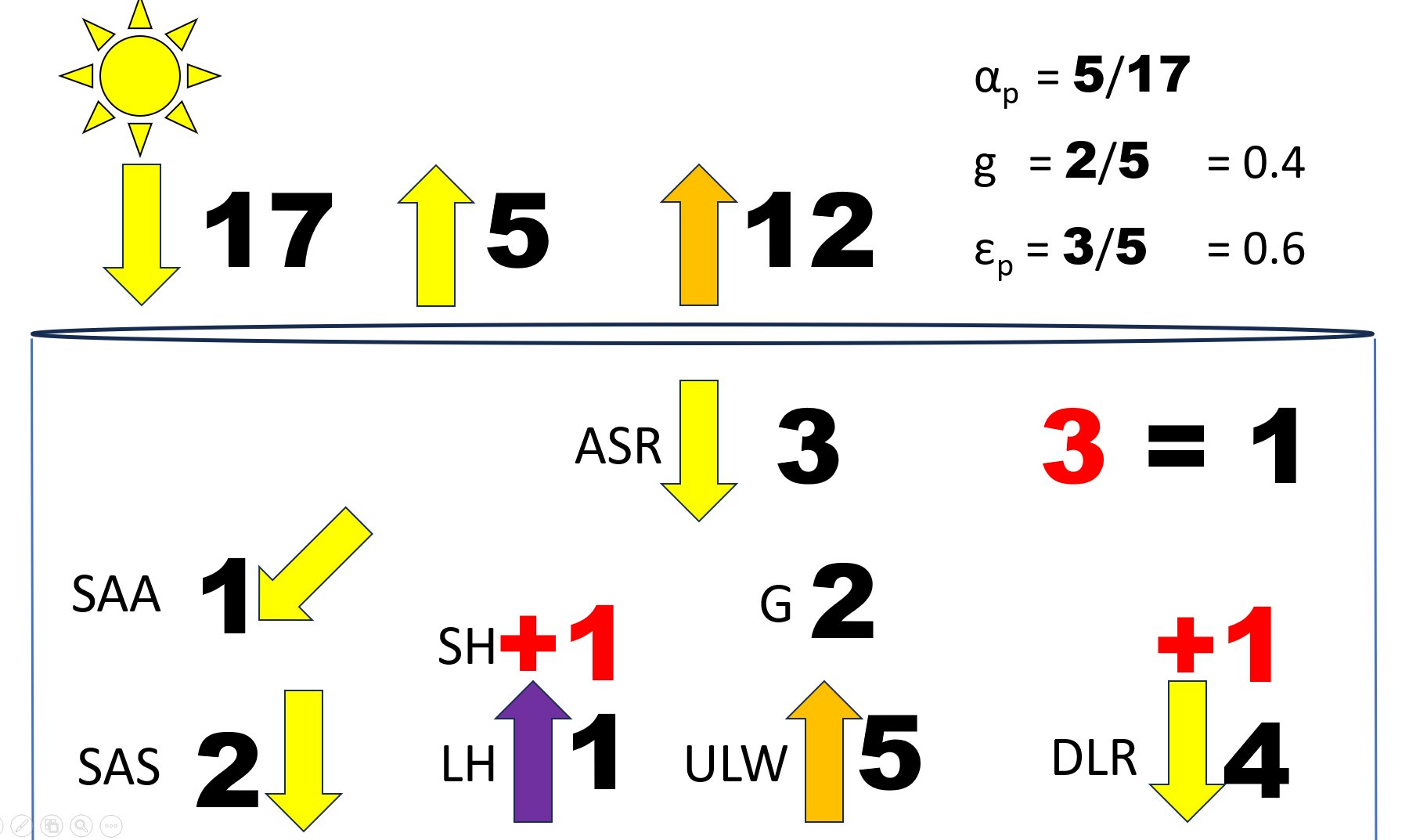
Then simply transform everything into red units, and you will see that the two all-sky equations (3) and (4) for the net radiation at the surface and the total radiation absorbed by the surface, shown for example in the GEWEX diagram, are satisfied, and each of the values fit exactly to their observed representatives:

Let's take a small prime number: let it be 17. This will be my Total Solar Irradiance, TSI = 17 units.
Let us allow 5 to be reflected. This way, we have a planetary albedo of 5/17, which is arithmetically identical to the value given by the IPCC AR6 diagram, where the all-sky TOA incoming solar radiation is 340, and the solar reflection is 100 Wm-2, hence their albedo is 100/340 = 5/17.
Another benefit is that the absorbed solar radiation is then 12 units, which, after spherical weigting (division by 4), results in 3 units absorbed solar and emitted LW radiation. Using the well-kown 1 : 2 : 1 model of the simplest greenhouse geometry in a solar-transparent and infrared-opaque atmosphere, we then have 3 uni ts solar absorbed surface, 6 units LW emitted upward by the surface, and again 3 units emitted LW downward by the atmosphere. Then introduce 1 unit of evaporation at the surfacen by decreasing upward longwave to 5 units.
I assign 80.04 Wm-2 to this 1 unit since I know in advance that it will become 3 units soon, with 1 unit = 26.68 Wm-2.
This structure is very similar to what we really have. TSI = 17 × 80.04 = 1360.68 Wm-2, while the most accurate value of TSI, according to Kopp and Lean (2011) is 1360.8 ± 0.5 Wm-2. The planetary emissivity is TOA LW / Surface ULW = 3/5 here, while in the IPCC AR6 Fig. 7.2 diagram it is 239/398 = 0.6005:

Now introduce 1 unit for solar absorbed by the atmosphere, therefore SAS decreases to 2 units, but DLR increases to 4 units:

Using the 'light-wieghted' quantum of 3 = 1, let me add 1 unit to DLR (since we are in the all-sky) as LWCRE, and to balance it by 1 unit added to convection as sensible heat:

Then simply transform everything into red units, and you will see that the two all-sky equations (3) and (4) for the net radiation at the surface and the total radiation absorbed by the surface, shown for example in the GEWEX diagram, are satisfied, and each of the values fit exactly to their observed representatives:

This
is really a very elementary 'quantum' decuction of the all-sky integer
system. This way we got an alternative approach to the all-sky albedo,
compared tostep (iii) in the opening page, where we started approaching
the clear-sky albedo by allowing 1 unit solar reflection out of 5 units
of incoming, but finally both leading to the correct
clear-sky
and all-sky TOA reflection.
But let me notice that from the previous diagram we may step into another direction as well. Let us remember that, according to step (vi) of the deduction on the opening page, clear-sky TOA Net Imbalance is 3 units (on the disk), therefore, after spherical weighting, 3/4 units in step (x), with a value of 20.01 Wm-2; consequently, in step (xii), in the all-sky, the net cloud radiative effect, TOA Net CRE was -3/4.
Now what if we take THIS one, this smaller, even 'lighter' quantity, TOA Net CRE, the new quantum, shown in green? 1 = 3/4 = 20.01 Wm-2.
Then we get the following structure:
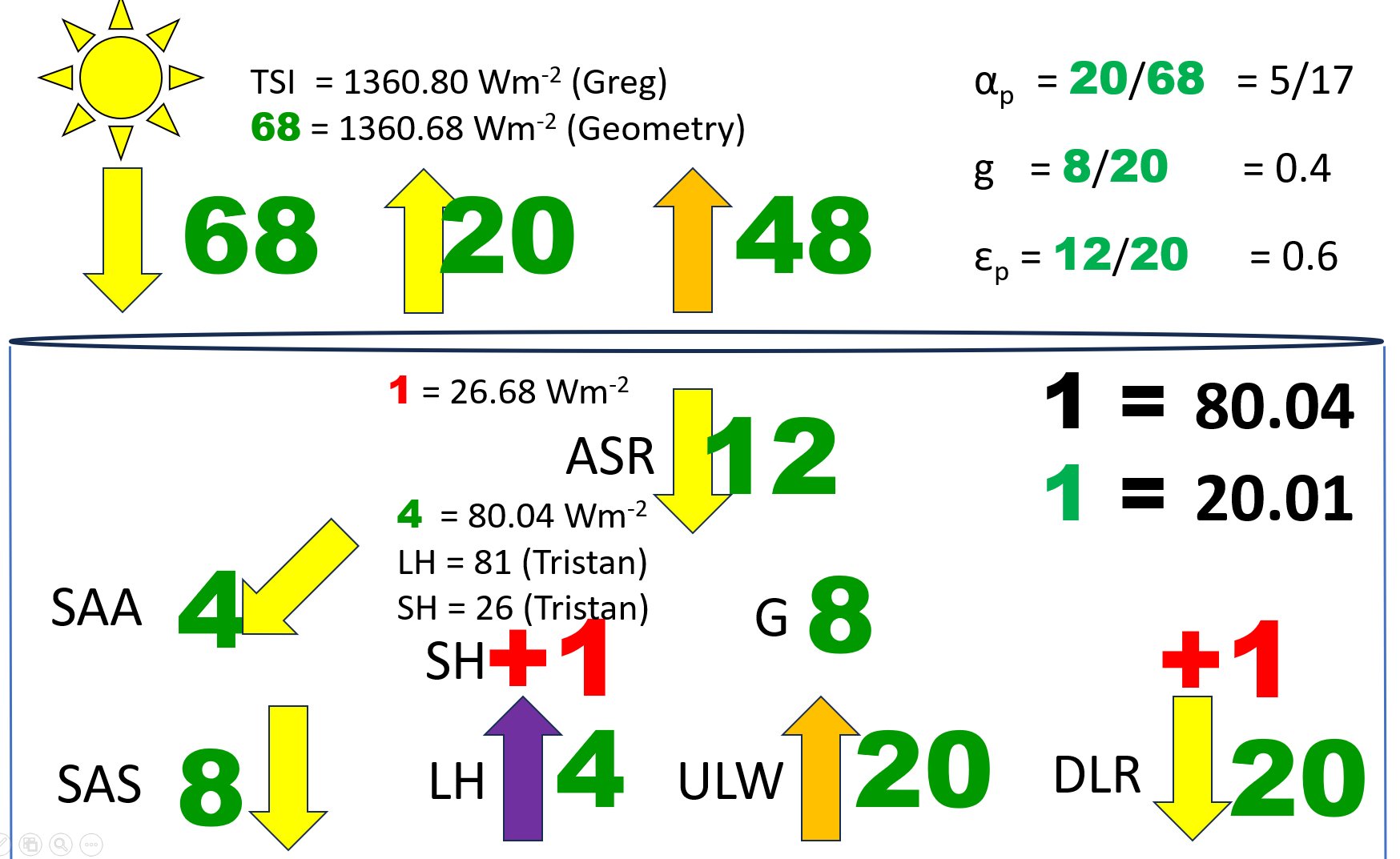
In this third, lighter, green quantum, 1 = TOA Net CRE = 20.01 Wm-2, each black unit became four green units, integer as well, even TSI (68) and solar reflection (20), moreover, evaporation (latent heat) as 4 units! And the all-sky structure requires red unit (LWCRE) only in downward longwave radiation (DLR) and one unit in sensible heat.
Three quanta: a heavy, a lighter and an even-lighter, as freely transforming into each other? Mind-blowing as it is!
Though this be madness yet there is method in 't.
But let me notice that from the previous diagram we may step into another direction as well. Let us remember that, according to step (vi) of the deduction on the opening page, clear-sky TOA Net Imbalance is 3 units (on the disk), therefore, after spherical weighting, 3/4 units in step (x), with a value of 20.01 Wm-2; consequently, in step (xii), in the all-sky, the net cloud radiative effect, TOA Net CRE was -3/4.
Now what if we take THIS one, this smaller, even 'lighter' quantity, TOA Net CRE, the new quantum, shown in green? 1 = 3/4 = 20.01 Wm-2.
Then we get the following structure:

In this third, lighter, green quantum, 1 = TOA Net CRE = 20.01 Wm-2, each black unit became four green units, integer as well, even TSI (68) and solar reflection (20), moreover, evaporation (latent heat) as 4 units! And the all-sky structure requires red unit (LWCRE) only in downward longwave radiation (DLR) and one unit in sensible heat.
Three quanta: a heavy, a lighter and an even-lighter, as freely transforming into each other? Mind-blowing as it is!
Though this be madness yet there is method in 't.